أسئلة إحصاء تالتة ثانوي 2025 أدبي للمراجعة النهائية

ينشر شبابيك أسئلة إحصاء تالتة ثانوي 2025 أدبي للمراجعة النهائية، حتى يتمكن الطلاب من الاستعداد الجيد لخوض الامتحان.

أعد عدد من معلمي المادة أسئلة على الإحصاء للثانوية العامة الشعبة الأدبية، حتى يتعرف الطلاب على شكل السؤال.

​​​​​​​

أسئلة إحصاء للثانوية العامة 2025 أدبي

جاءت أسئلة مادة الإحصاء للصف الثالث الثانوي الشعبة الأدبية 2025 على النحو التالي:

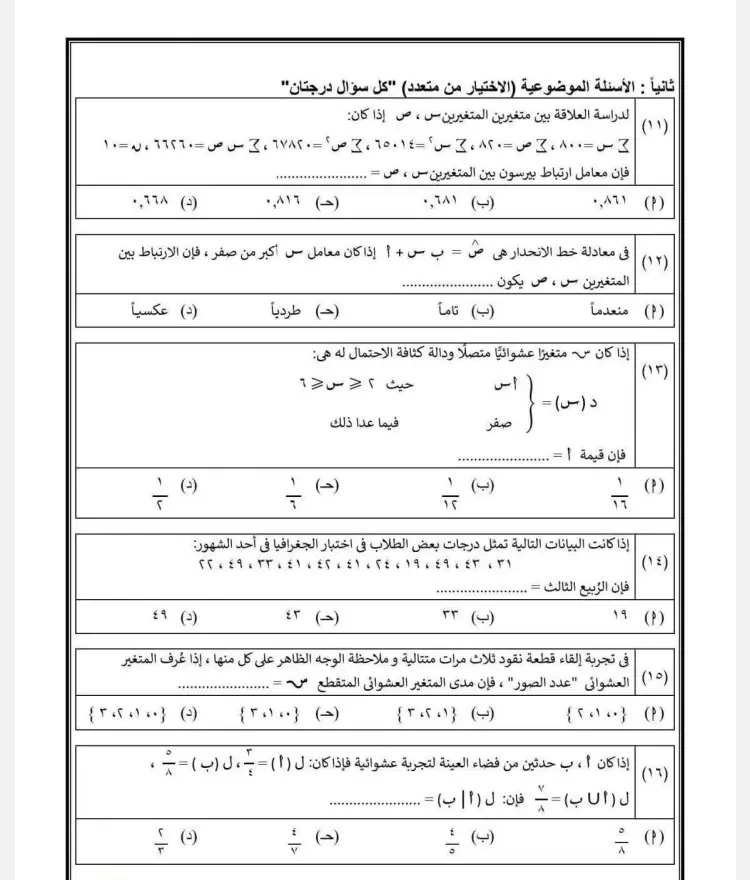
١) لدراسة العلاقة بين المتغيرين س ، ص إذا كان:
ك = ∑س = ٨٢ ، ∑ص = ١٥١ ، ∑س² = ١٢٨٤٫٨ ، ∑ص² = ٢٢٨٧٫٢ ، ∑س ص = ١٣٦٦٫٢ ، ن = ١٠
فإن معامل ارتباط بيرسون بين المتغيرين س ، ص = ........
(أ) ٠٫٨٦١
(ب) ٠٫٨٦٨
(ج) ٠٫٨١٦
(د) ٠٫٨١٢

٢) إذا كانت معادلة خط الانحدار هي ص = ب س + أ، إذا كان معامل س أكبر من صفر، فإن الارتباط بين المتغيرين س، ص يكون:
(أ) متناسبًا
(ب) تامًا
(ج) طرديًا
(د) عكسيًا

٣) إذا كان س متغيرًا عشوائيًا متصلاً ودالة كثافة الاحتمال له هي:
د(س) = { ٢ س ≥ ٠
٠ س < ٠ }
فما قيمة ∫ د(س) دس = ............
(أ) ١
(ب) ١/٢
(ج) ٢
(د) ٠

٤) إذا كانت البيانات التالية تمثل درجات بعض الطلاب في اختبار الجغرافيا في أحد الشهور:
٤٣ ، ٤١ ، ٤٣ ، ٤٤ ، ٤٩ ، ٤٢ ، ٤١ ، ٤٤ ، ٤٣ ، ٤٢
فإن الربيع الثالث = ............
(أ) ٣٣
(ب) ٤٢
(ج) ٤٣
(د) ٤٩

٥) في تجربة إلقاء قطعة نقود ثلاث مرات متتالية وملاحظة الوجه الظاهر على كل منها، إذا عُرف المتغير العشوائي "عدد الصور"، فإن مدى المتغير العشوائي المتقطع س = ............
(أ) { ٠ ، ١ ، ٢ ، ٣ }
(ب) { ١ ، ٢ ، ٣ }
(ج) { ١ ، ٣ }
(د) { ٠ ، ١ ، ٢ }

٦) إذا كانت ل من فضاء العينة لتجربة عشوائية فإذا كانت:
ل(أ) = ٢/٨ ، ل(ب) = ٣/٨
فإن: ل (أ ∪ ب) = ............
(أ) ٢/٨
(ب) ٤/٨
(ج) ٥/٨
(د) ٧/٨

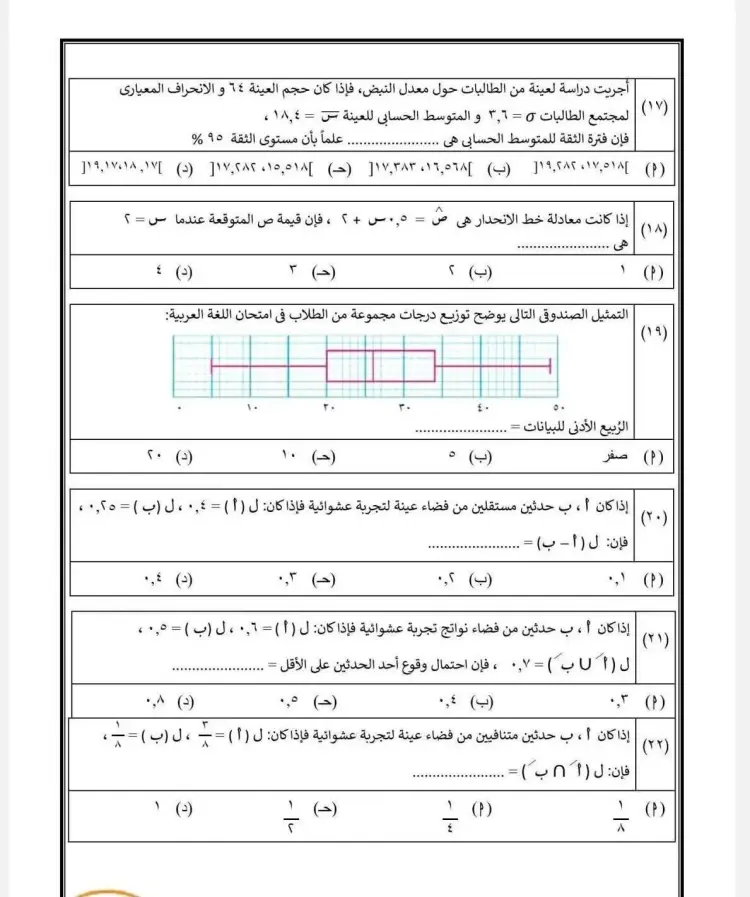
٧) أجريت دراسة لعينة من الطالبات حول معدل النبض، فإذا كان حجم العينة = ١٤، والانحراف المعياري لمجتمع الطالبات σ = ٦، و المتوسط الحسابي للعينة = ١٨٫٤
فإن فترة الثقة للمتوسط الحسابي μ علـى أن مستوى الثقة ٩٥٪ هي ............
(أ) [١٣٫٢٧٥ ، ٢٣٫٥٢٥]
(ب) [١٣٫٨٢٨ ، ٢٣٫٤٢]
(ج) [١٣٫٦١٣ ، ٢٣٫١٨٧]
(د) [١٣٫٧٥٤ ، ٢٣٫٤٦]

٨) إذا كانت معادلة خط الانحدار هي ص̂ = ٠٫٥ س + ٢، فإن قيمة ص̂ المتوقعة عندما س = ٢ هي ............
(أ) ٢
(ب) ٣
(ج) ٤
(د) ١

٩) التمثيل الصندوقي التالي يوضح توزيع درجات مجموعة من الطلاب في امتحان اللغة العربية:
الربيع الأدنى للبيانات = ............
(أ) ٠
(ب) ٥
(ج) ١٠
(د) ٢٠

١٠) إذا كان أ ، ب حدثين مستقلين من فضاء عينة لتجربة عشوائية فإذا كان:
ل(أ) = ٠٫٤ ، ل(ب) = ٠٫٥
فإن: ل (أ ∩ ب) = ............
(أ) ٠٫٢
(ب) ٠٫٣
(ج) ٠٫٢٥
(د) ٠٫١

١١) إذا كان أ ، ب حدثين من فضاء نواتج تجربة عشوائية فإذا كان:
ل(أ) = ٠٫٦ ، ل(ب) = ٠٫٥ ، ل(أ ∩ ب) = ٠٫٢
فإن احتمال وقوع أحد الحدثين على الأقل = ............
(أ) ٠٫٨
(ب) ٠٫٥
(ج) ٠٫٤
(د) ١

١٢) إذا كان أ ، ب حدثين متنافيين من فضاء عينة لتجربة عشوائية فإذا كان:
ل(أ) = ٣/٨ ، ل(ب) = ٢/٨
فإن: ل(أ ∪ ب) = ............
(أ) ١
(ب) ٦/٨
(ج) ١/٢
(د) ٥/٨