حل امتحان الجبر للصف الثالث الإعدادي الترم الأول 2026 الغربية بالخطوات
ينشر شبابيك نموذج إجابة امتحان مادة الجبر والإحصاء للشهادة الإعدادية بمحافظة الغربية عن الفصل الدراسي الأول للعام التعليمي 2025-2026.
إجابات امتحان الجبر تالتة إعدادي الغربية ترم أول 2026
تألف الاختبار من 3 ورقات للحل مثال الأسئلة الواردة فيه ما يلي:
السؤال الأول:
1- الثالث المتناسب بين 5، 10 هو ........... (أ: 5، ب: 10، ج: 20، د: 50)
2- إذا كانت d(x)=4x+b وكانت d(3)=15 فإن قيمة b=… (أ: 2، ب: 3، ج: 15، د: صفر)
3- الدالة d(x)=(x−3)2 دالة كثيرة حدود من الدرجة ........... (أ: الثانية، ب: الأولى، ج: الصفرية، د: الرابعة)
4- إذا كانت النقطة (3,b−5) تقع على محور السينات فإن 2b+1=… (أ: صفر، ب: 5، ج: 11، د: 8)
5- إذا كان 3x=5y فإن y∝… (أ: x، ب: x1، ج: x+3، د: x−5))
6- إذا كان (2x,4)=(8,y+1) فإن x2+y2=… (أ: 9، ب: 25، ج: 3، د: 5)
7- إذا كان (6,4)∈{3,x}×{8,4} فإن x=… (أ: 8، ب: 6، ج: 4، د: 3)
8- عدد المجموعات الجزئية من المجموعة S={1,2} تكون ........... (أ: 2، ب: 6، ج: 4، د: 8)
9- إذا كان 2−x=5 فإن 22x=… (أ: 10، ب: 7، ج: 16، د: 1/25) (ملاحظة: الخيار د غير واضح تماماً بالصورة لكنه منطقياً 1/25).
حل الاختبار كاملا
(الاختيار من متعدد):
(ج) 20: لأن 105=x10⟹5x=100⟹x=20.
(ب) 3: 4(3)+b=15⟹12+b=15⟹b=3.
(أ) الثانية: لأن فك القوس يعطي x2−6x+9.
(ج) 11: تقع على محور السينات يعني y=0⟹b−5=0⟹b=5. إذن 2(5)+1=11.
(أ)) x: لأن y=53x (تغير طردي.
(د) 5: 2x=8⟹x=4؛ y+1=4⟹y=3. إذن 42+32=25=5.
(ب) 6: المسقط الأول 6 يجب أن ينتمي للمجموعة الأولى {3,x}، إذن x=6.
(ج) 4: المجموعات هي ϕ,{1},{2},{1,2}. والقانون 2n=22=4.
(1/25): 2x=51⟹(2x)2=(51)2=251.
(الأسئلة المقالية):
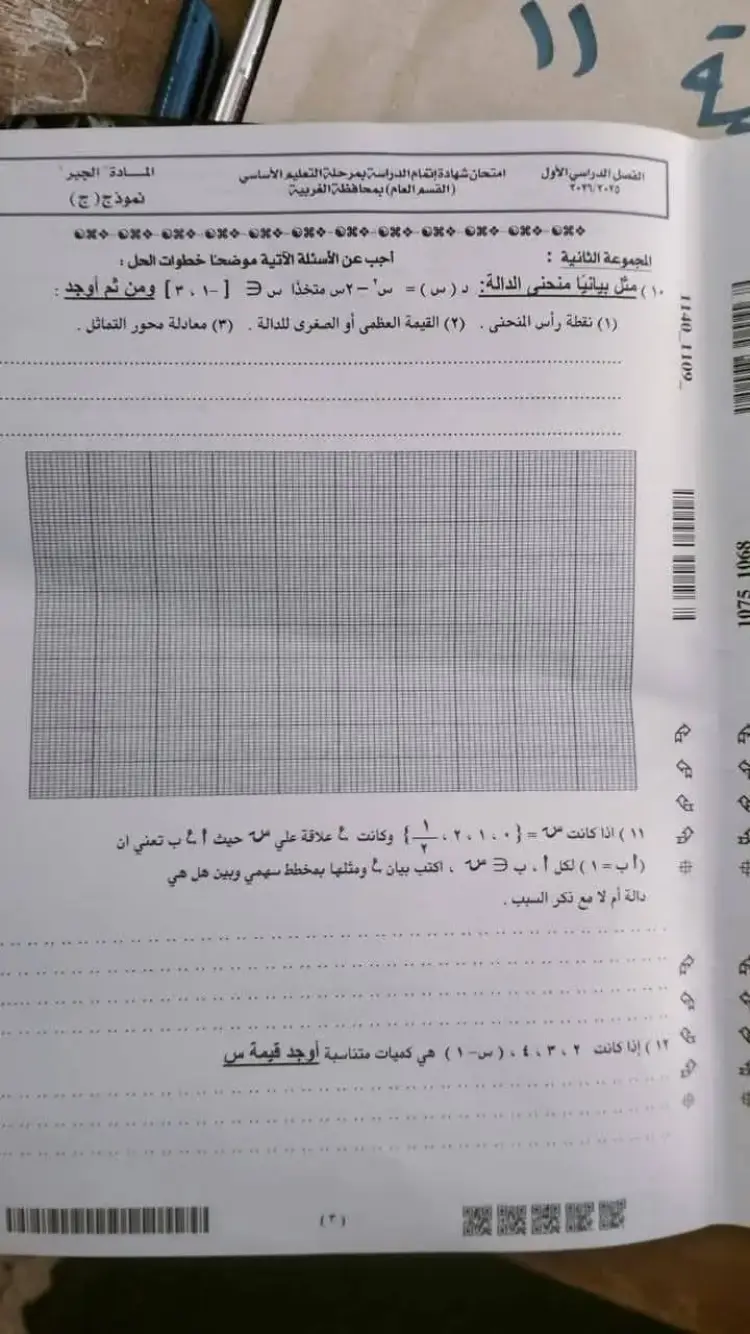
س10: التمثيل البياني لـ d(x)=x2−2x في الفترة [−1,3]
النقاط: d(−1)=3,d(0)=0,d(1)=−1,d(2)=0,d(3)=3.
(1) نقطة رأس المنحنى: (1,−1).
(2) القيمة الصغرى: −1.
(3) معادلة محور التماثل: x=1.
س11: العلاقة R حيث a×b=1 على المجموعة X={21,0,1,2}
بيان العلاقة: R={(2,21),(1,1),(21,2)}.
ليست دالة: لأن العنصر (0) لم يخرج منه سهم (ليس له معكوس ضربي).
س12: كميات متناسبة 2، 3، 4، (س-1)
32=x−14⟹2(x−1)=12⟹x−1=6⟹x=7.
س13: إثبات تناسب ب وسط متناسب بين أ، ج ⟹b2=ac أو ba=cb=m⟹b=cm,a=cm2.
الطرف الأيمن: a−ca−b=cm2−ccm2−cm=c(m−1)(m+1)cm(m−1)=m+1m.
الطرف الأيسر: b+cb=cm+ccm=c(m+1)cm=m+1m.
إذن الطرفان متساويان.
س14: أ، 3، 9، ب في تناسب متسلسل
3a=93=b9.
3a=31⟹a=1.
93=b9⟹31=b9⟹b=27.
قيمة b−12=27−12=15.
س15: التغير الطردي
y=kx⟹6=k9⟹6=3k⟹k=2.
أولاً: العلاقة هي y=2x.
ثانياً: عندما x=4⟹y=24=2×2=4.
س16: الوسط الحسابي والانحراف المعياري للقيم (13، 14، 17، 19، 22)
الوسط (xˉ) = 513+14+17+19+22=585=17.
الانحراف (σ):
(13−17)2=16
(14−17)2=9
(17−17)2=0
(19−17)2=4
(22−17)2=25
مجموع المربعات = 16+9+0+4+25=54.
σ=554=10.8≈3.28.