مراجعة بحتة تانية ثانوي الترم الثاني 2025 في 6 ورقات فقط
يبحث كثير من طلبة الشعبة العلمية عن مراجعة بحتة تانية ثانوي الترم الثاني 2025 استعدادا لامتحانات نهاية السنة الدراسية 2024 2025.
مراجعة بحتة تانية ثانوي الترم الثاني
ويستعد كثير من الطلاب لامتحانات الفصل الدراسي الثاني والتي تقام في مايو الجاري.
ويأمل كثير من الطلاب في إيجاد مراجعة بحتة تانية ثانوي الترم الثاني 2025، وتشمل تلخيص أهم النقاط في المنهج.
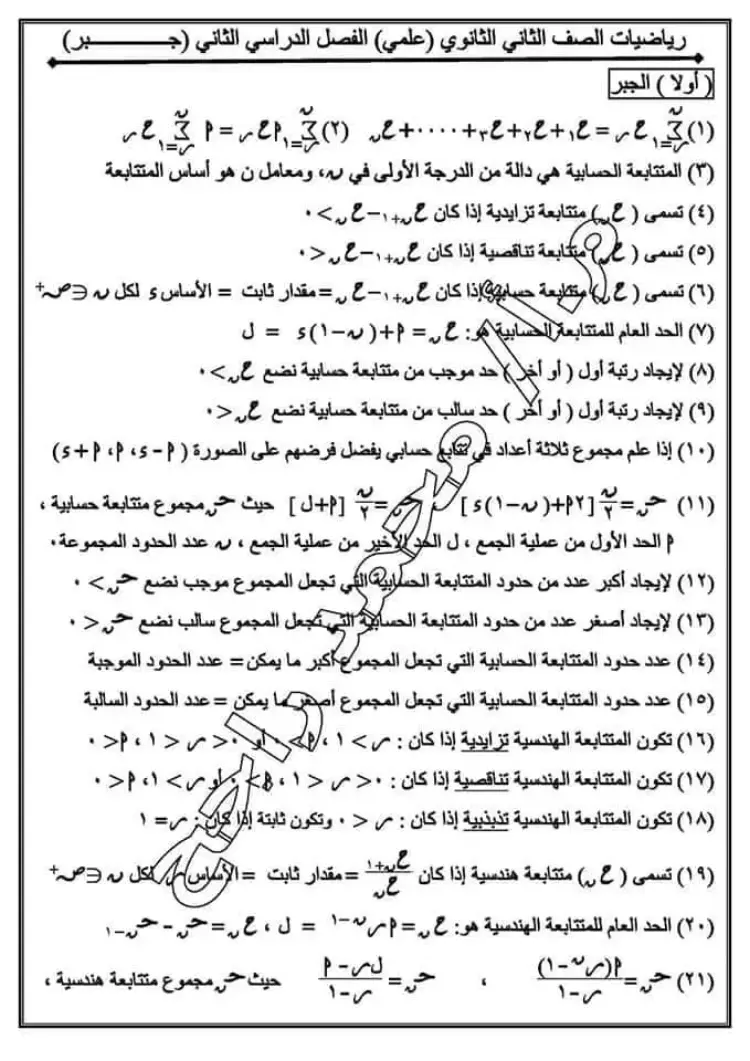
وتضم تلك المذكرة أهم نقاط منهج الرياضيات البحتة للصف الثاني الثانوي في 6 ورقات فقط.
وإليكم في هذه السطور مراجعة بحتة تانية ثانوي الترم الثاني 2025:
١) ص، ص + ع، ص + ٢ع، ص + ٣ع، ... ص + (ن-١)ع
يُرمز لها بـ ح ن = ص + (ن-١)ع
٢) المتتابعة الحسابية هي دالة من الدرجة الأولى في ن، ومعامل ن هو أساس المتتابعة.
٣) تُسمى ح ن متتابعة تزايدية إذا كان ع > ٠، ح ن+١ > ح ن
٤) تُسمى ح ن متتابعة تناقصية إذا كان ع < ٠، ح ن+١ < ح ن
٥) تُسمى ح ن متتابعة ثابتة إذا كان ع = ٠، ح ن+١ = ح ن
٦) الحد النوني للمتتابعة الحسابية: ح ن = ص + (ن-١)ع
٧) المجموع لحدود متتابعة حسابية: جـ ن = ن / ٢ × [٢ص + (ن-١)ع]
أو جـ ن = ن / ٢ × (ح١ + ح ن)
٨) إذا علم مجموع ثلاث أعداد في متتابعة حسابية ومضاعفهم على الترتيب (ص - ع، ص، ص + ع)
فإن: جـ = ٣ص
٩) جـ = ن / ٢ × [٢ص + (ن-١)ع] حيث جـ مجموع متتابعة حسابية
ص: الحد الأول من عملية الجمع
ن: عدد الحدود المجموعة
ع: عدد من حدود المتتابعة الحسابية
١٠) لإيجاد أكبر عدد من حدود المتتابعة الحسابية التي تجعل المجموع لا يتعدى ح > جـ
١١) لإيجاد أصغر عدد من حدود المتتابعة الحسابية التي تجعل المجموع أكبر من جـ > ح
١٢) عدد حدود المتتابعة الحسابية التي تعين المجموع يمكن إيجاده بحل المعادلة التربيعية
١٣) عدد الحدود السالبة التي تجعل المجموع < ٠ يمكن أن تكون المتتابعة سالبة.
١٤) تُسمى ح ن متتابعة هندسية تزايدية إذا كان: ن > ١، ح ن+١ > ح ن
١٥) تُسمى ح ن متتابعة هندسية تناقصية إذا كان: ٠ < ن < ١، ح ن+١ < ح ن
١٦) تكون المتتابعة الهندسية ثابتة إذا كان ن = ١، وتكون ثابتة إلا حدًا واحدًا.
١٧) ح ن = ص ن-١
حيث ص: الحد الأول
ن: عدد الحدود
ن: أساس المتتابعة الهندسية
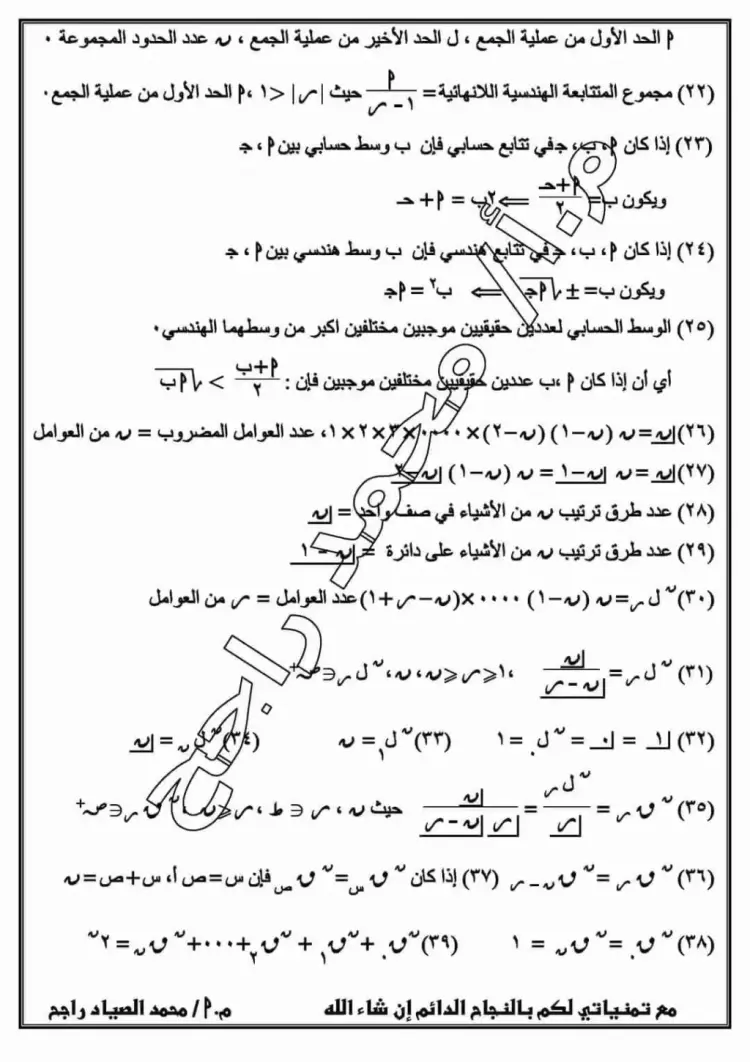
١٨) الحد العام للمتتابعة الهندسية هو: ح ن = ص × نⁿ⁻¹
د = ل ÷ ص، ح ن = ص × نⁿ⁻¹
١٩) جـ ن = ص(١ - نⁿ) ÷ (١ - ن)، ن ≠ ١
حيث جـ ن مجموع متتابعة هندسية