مطوية المعادلات الخطية ثالث متوسط

يبحث الطلاب وأولياء الأمور عن كيفية عمل مطوية المعادلات الخطية ثالث متوسط، وذلك لتقديمها في مادة الرياضيات، كأحد المتطلبات الدراسية، كما تساعد المطوية على تثبيت المعلومات. 

مطوية المعادلات الخطية ثالث متوسط

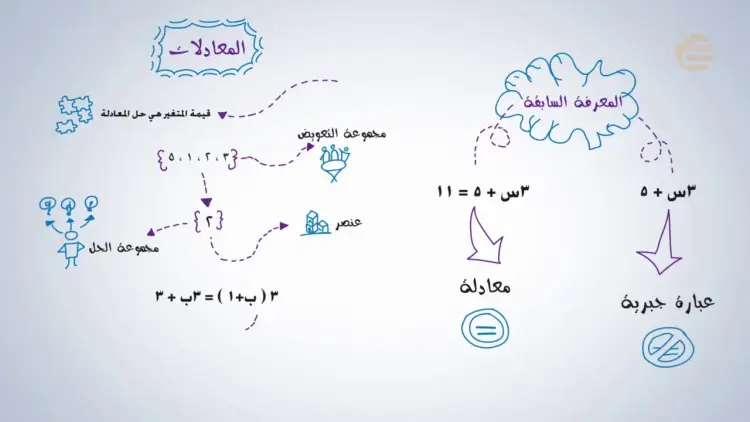
تمثل مطوية المعادلات الخطية للصف الثالث متوسط أداة مبسطة تهدف إلى توضيح المفاهيم الأساسية الخاصة بالمعادلات الجبرية من الدرجة الأولى.

وتعرض المطوية الأفكار النظرية والأمثلة العملية بطريقة منظمة عبر أربعة أوجه رئيسية، ما يساعد الطلاب على فهم خطوات الحل وتطبيقها في المقررات الدراسية.

أدوات مطوية المعادلات الخطية ثالث متوسط

إعداد «مطوية المعادلات الخطية» يتطلب توفير أدوات بسيطة لتسهيل تنفيذها:

• ورق مقوى أو ملون: أساس المطوية.

• أقلام ألوان أو طباعة بالصور: لإبراز خطوات الحل والرسوم البيانية.

• مقص ومسطرة وغراء: لتقسيم الورقة إلى الأوجه الأربعة.

• رسوم توضيحية: لعرض الخطوط المستقيمة والتمثيلات البيانية بشكل مبسط.

كيفية عمل مطوية المعادلات الخطية ثالث متوسط

خطوات إعداد المطوية تتمثل في:

• تحديد الأهداف التعليمية: التركيز على تعريف المعادلات الخطية، طرق الحل، والتمثيل البياني.

• طي الورقة: تقسيمها إلى أربعة أوجه لعرض محتوى متدرج.

• توزيع الموضوعات: تخصيص كل وجه لموضوع محدد.

• إضافة أمثلة ورسومات: عرض مسائل محلولة وتمثيلها بيانياً.

• مراجعة المحتوى: التأكد من دقة الشرح ومطابقته للمنهج السعودي.

نموذج كامل لمطوية المعادلات الخطية ثالث متوسط

يظهر النموذج المقترح المطوية في شكل كتيب تعليمي صغير، يبدأ بالتعريفات الأساسية، يوضح التمثيل البياني، يقدم التطبيقات اليومية، ويختتم بالأمثلة والحلول، يعتمد على عرض النقاط بطريقة منظمة مع مساحة مخصصة لتدريب الطلاب.

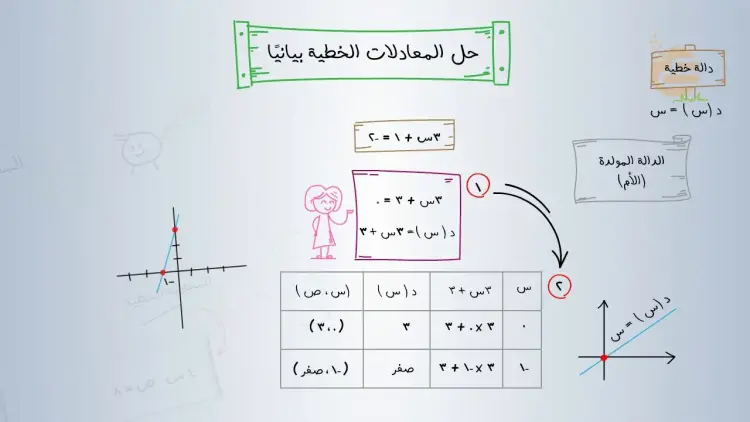
الوجه الأول لمطوية المعادلات الخطية ثالث متوسط

• تعريف المعادلة الخطية: هي معادلة جبرية من الدرجة الأولى.

• الصيغة العامة في متغير واحد: ax+b=0ax + b = 0ax+b=0 حيث a≠0a \neq 0a=0.

• الصيغة العامة في متغيرين: ax+by+c=0ax + by + c = 0ax+by+c=0 حيث aaa و bbb لا يساويان معًا الصفر.

الوجه الثاني لمطوية المعادلات الخطية ثالث متوسط

• التمثيل البياني: يتمثل في رسم خط مستقيم يوضح جميع الأزواج المرتبة التي تحقق المعادلة.

• أنظمة المعادلات الخطية:

  • نظام متسق له حل وحيد: تقاطع خطين في نقطة.

  • نظام متسق له حلول لا نهائية: تطابق الخطين.

  • نظام غير متسق: توازي الخطين.

الوجه الثالث لمطوية المعادلات الخطية ثالث متوسط

• تطبيقات المعادلات الخطية:

  • حساب التكاليف باستخدام معادلات من الدرجة الأولى.

  • تحديد المسافة وفق العلاقة «السرعة × الزمن».

  • مقارنة الأسعار أو الأرباح بين مؤسستين.

  • حل مسائل حياتية تعتمد على العلاقات الرياضية البسيطة.

الوجه الرابع لمطوية المعادلات الخطية ثالث متوسط

• أمثلة في متغير واحد:

  • حل المعادلة 3x−5=103x - 5 = 103x−5=10.

  • الحل: 3x=153x = 153x=15 ثم x=5x = 5x=5.

• أمثلة في متغيرين:

  • النظام:

    • x+y=6x + y = 6x+y=6

    • x−y=2x - y = 2x−y=2

  • بالجمع: 2x=82x = 82x=8 إذن x=4x = 4x=4 و y=2y = 2y=2.